Last time, I have shared the first results obtained by the LTN on the conceptual space of movies. Today, I want to give you a quick update on the first membership function variant that I have investigated.
Remember from my earlier blog post, that the standard membership function used in vanilla LTNs does not enforce convexity – based on the distribution of the training data points, the LTN might end up learning a non-convex membership function as illustrated in Figure 1:
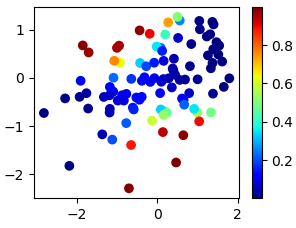
In my earlier blog post, I analyzed why this can happen and how we can fix this. I proposed a slight modification to the formula of the membership function that solves this problem.
While this might be satisfying from a theoretical point of view, it is not yet clear whether this is actually useful in practice: If the data points form convex clusters anyways, then also the vanilla LTN should be able to learn convex membership functions. In order to see whether the modification of the membership function makes any difference, I have run the experiments reported last times with the modified LTN. Let’s see what the results look like.
Table 1: Does enforcing a convex memberhsip function change anything?
| Metric | Test set performance convex LTN | Test set performance vanilla LTN | Test set performance kNN |
|---|---|---|---|
| One Error | 0.2131 | 0.2150 | 0.1597 |
| Coverage | 5.1704 | 5.1972 | 5.5876 |
| Ranking Loss | 0.0798 | 0.0806 | 0.0558 |
| Cross Entropy Loss | 11.9423 | 11.9926 | 82.3033 |
| Average Precision | 0.7784 | 0.7772 | 0.8014 |
| Exact Match Prefix | 0.1444 | 0.1439 | 0.1672 |
| Minimal Label-Wise Precision | 0.4494 | 0.4546 | 0.1931 |
| Average Label-Wise Precision | 0.6280 | 0.6291 | 0.4931 |
Table 1 compares the performance on the test set between the best convex LTN, the best vanilla LTN, and the best kNN. We do of course observe slight variations between the two LTN variants, but it seems that they yield very similar performance on all the metrics. As we are unable to see any systematic and considerable differences, we are probably safe to assume that they both end up learning very similar membership functions. The observed differences should then be attributed to random noise (like the different random initialization of the networks’ weights).
So it seems like the data points in the movie space already form convex clusters (as we would by the way anyways expect in a conceptual space). In our experiments on these data sets, it therefore makes no difference whether we use vanilla LTNs or convex LTNs.
What’s next?
Based on what I said before, you probably expect more results for all the other membership functions in the next weeks. That’s however not going to happen.
Why?
Well, I had a Skype call with Luciano Serafini and Michael Spranger (two of the main LTN people out there) the other day and they have pointed out some weaknesses in my approach: They suggested to use additional evaluation metrics and to introduce stronger competitors than the kNN. Moreover, my experiments were run with the very first version of LTNs, but there’s a more efficient and better-engineered version available these days. Last but not least, I’m currently not using any background knowledge in the training process – but that’s exactly one strong suit of LTNs when being compared to more classical machine learning algorithms.
Long story short – I need to redesign my experimental setup in order to get more robust and more meaningful results. So I stopped all my current experiments for now. My next blog post on LTNs will then explain the new setup once I’ve figured it out.
