Since my current ANN experiments are moving forward rather slowly, I have spent some time preparing the final background chapter for my dissertation. I the course of doing so, I have among other things looked at COBWEB [1], which is one of the most well-known concept formation algorithms. Today, I want to share the basic idea behind COBWEB and its variants.
Concept Formation in General
Quite some time ago, I have provided a rough sketch of concept formation in general. Here’s a quick recap based on [2]: In concept formation, we observe unlabeled examples one after another and try to find a clustering of these examples into categories, which are then organized in a conceptual hierarchy. Moreover, each category is not represented as a set of examples, but based on abstracted information about typical feature values. Concept formation algorithms typically follow an incremental hill-climbing process, where the conceptual hierarchy is updated after each observation.
Representation in COBWEB
How are concepts and the conceptual hierarchy defined in COBWEB? The overall conceptual hierarchy is represented as a tree and each inner node corresponds to one concept. A concept is specified through three types of conditional probability distributions:
- The predictability p(value|concept) represents the distribution of possible feature values for members of the concept: If you know that the observation x belongs to the concept C, which kind of feature values v do you expect it to have?
- The predictiveness p(concept|value) on the other hand tells us how indicative a certain feature value is for concept membership: If observation x has the feature value v, does this tell us anything about its membership to concept C?
- The relative frequency p(concept|parent) tells us how frequent this concept is in comparison to its “siblings” in the hierarchy: Given that the observation x belongs to the parent concept P, how likely is it that x also belongs to C?
These three types of conditional probability distributions can all be estimated based on raw co-occurrence counts from the observed examples: For instance, the predictability p(value|concept) can be approximated by counting the frequency of all feature values observed for all examples falling under the concept C and then normalizing these absolute counts. Updating a concept description thus simply corresponds to updating those counts, which then directly influences the probability distributions.
Category Utility
In order to measure how well a given conceptual hierarchy captures the underlying structure of the data, COBWEB uses an evaluation metric called “Category Utility”. I will spare you with the mathematical details (those are nicely laid out in both [1] and [2]), and limit myself to providing a rough intuition.
Category utility is inspired by the basic level of categorization in human classification hierarchies, where one in general has a good balance between intra-class similarity (i.e., examples of the same concept are similar) and inter-class dissimilarity (i.e., examples from different concepts are different). In COBWEB, this is formalized by a combination of predictability (do members of the same concept have the same feature values?) and predictiveness (are these feature values specific to the current concept or do they also apply to other concepts?).
As it turns out, combining predictability and predictiveness is mathematically equivalent to calculating the expected number of feature values that can be guessed correctly for an arbitrary example of the given category. Category utility is now defined as the increase in prediction performance that one gets from knowing the category membership of the data points. In other words, category utility quantifies how much the induced category structure helps to predict feature values better than chance.
Learning in COBWEB
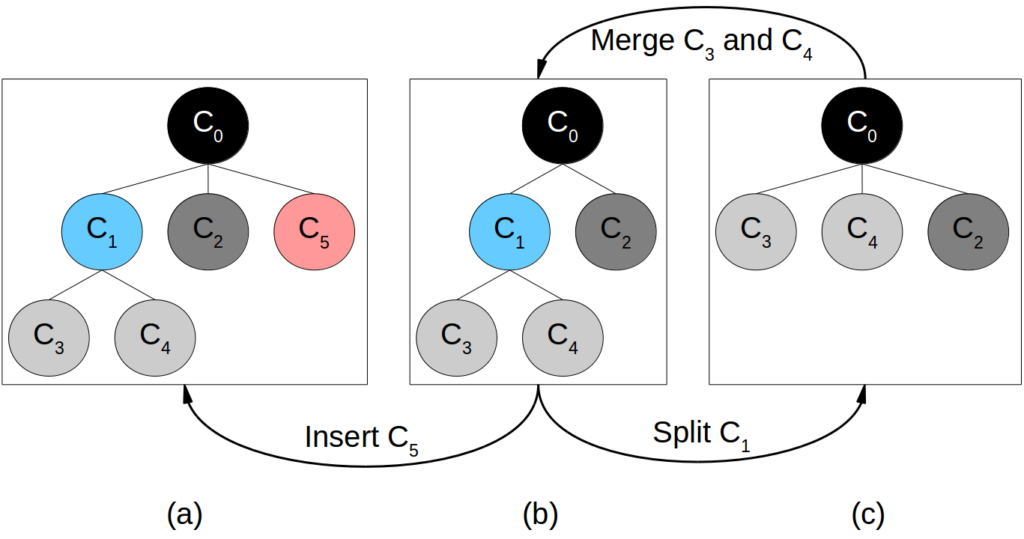
Okay, so how does COBWEB construct its conceptual hierarchy? Well, initially it starts with a single (empty) concept. Each new observation descends the tree in a top-down manner along the most appropriate branch (modifying the counts along the way) and at each level of the tree, one of the four following operators is used:
- Insert a new child concept: Create a new child concept and place the observation into this new child concept. In Figure 1, this results in a modification of the concept hierarchy from (b) to (a).
- Merge two child concepts: Take the two most appropriate child concepts and merge them – the original child concepts then become “grandchild” concepts under the newly created merged concept. In Figure 1, we can transition from the concept hierarchy in (c) to the one in (b) by merging C3 and C4.
- Split a child concept: Remove a child concept from the concept hierarchy altogether and promote its children to the next-higher level. In Figure 1, this corresponds to the change from (b) to (c), where C1 is removed and C3 and C4 become child concepts of C0.
- Add the observation to the best matching child concept: Simply select the most appropriate child concept and put the observation there, without modifying the conceptual hierarchy at all.
How does COBWEB decide which operator to use? Well, essentially it tries out all four of them and simply uses the one which results in the highest category utility. Please note that merging and splitting can be thought of as reverse operators. This allows COBWEB to correct for mistakes it made on earlier turns and makes the concept hierarchy thus more flexible.
CLASSIT for Continuous Features
COBWEB itself is limited to categorical features. Since I however deal with continuous dimensions in my conceptual spaces, I would first need to discretize them, e.g., by using properties from the individual domains as features. COBWEB would then go ahead and discover concepts spanning multiple domains based on the properties. However, in this scenario I already need to know the properties a priori, which prevents me from learning them in parallel to the cross-domain concepts.
Also Gennari et al. [2] have noticed this weakness of COBWEB and have proposed a variant called CLASSIT, which assumes continuous features. Instead of storing counts for the different feature values as a concept representation, CLASSIT uses one normal distribution per concept and feature. The mean and variance of this normal distribution can also be estimated in an incremental fashion, resorting to moving averages. CLASSIT comes with a generalized version of category utility that is applicable to non-categorical features as well.
Conceptual Spaces
The original goal of my PhD project was to develop a concept formation algorithm for conceptual spaces. As it turns out, I was sucked into so many other interesting subprojects that I didn’t have the time to work on concept formation. Nevertheless, the formalization of conceptual spaces that I have developed should in principle be able to support a concept formation algorithm similar to COBWEB and CLASSIT:
Instead of feature counts or normal distributions, the representation of each concept would be based on a fuzzy star-shaped set. The operations of splitting a concept (based on a threshold on a single dimension) and merging two concepts (by taking their union) are directly supported by my formalization. Incrementally adapting the concepts however would be more complex, since instead of updating counts or estimates of the mean and variance, one would need to modify the domain weights, the size and position of the individual cuboids, and the overall sensitivity parameter of the concept. Also the definition of category utility probably would need to be adapted to my scenario.
Overall, concept formation is in my opinion an important approach to concept learning, since it does not required labeled data and processes observations in an incremental fashion. Both of these aspects make it cognitively more plausible than classical supervised machine learning techniques that are based on batch-processing large labeled data sets.
References
[1] Fisher, D. H. Knowledge Acquisition via Incremental Conceptual Clustering Machine Learning, Springer Nature, 1987, 2, 139-172
[2] Gennari, J. H.; Langley, P. & Fisher, D. Models of Incremental Concept Formation Artificial Intelligence, Elsevier BV, 1989, 40, 11-61
