Imprecise concept boundaries with fuzzy sets

In my last blog post, I explained the underlying idea of my formalization of the conceptual spaces framework. At the end of the text, I made the remark:

There’s one little detail left, and I’ll cover it in my next blog post. It is the problem of imprecise concept boundaries.

This problem is probably best explained by an example: Suppose we would like to define the meaning of “tall person”. Let’s say we call everybody who has a height of at least 1.80 m “tall”, and everybody below this threshold “not tall”. Why is this problematic?

Well, imagine that one of your friends (let’s call him Andrew) is exactly 1.80 m, whereas another one of your friends (let’s call him Bob) is exactly 1.79 m. One would expect that Bob would be reasonably unhappy about our definition of “tall”. After all, you can barely tell the difference between his height and Andrew’s height. So why should one of them be called “tall” and the other one not? “All right”, you might say, “let’s change our threshold to 1.79 m”. But what happens if the next person (let’s say Charles) comes along with a height of 1.78 m? We would again need to change our definition. If we keep playing this game, we probably end up saying that everyone with a height of at least 0.00 m is considered to be “tall” – which clearly does not make too much sense.

The underlying problem is that we are forced to make a binary decision – somebody is either tall or not tall. And no matter where you put the boundary of your “tall person” concept, you will always be able to construct counter-examples. So what do we do?

One possible solution to this problem comes in the form of so-called “fuzzy sets” [1]. Fuzzy sets are a generalization of ordinary (“crisp”) sets. Whenever you define a crisp set, you can give a rule that states which objects should be in the set, for example “the set of all numbers between 42 and 1337”. By applying this rule, you can then derive the elements of the set. One could say that all numbers that fulfill this rule are full members of the set and get a membership value of 1.0, and all numbers that don’t fulfill this rule are not in the set and get a membership value of 0.0.

The key idea of fuzzy sets is now that we can in theory also allow partial memberships to a set, i.e., membership values between 0 and 1. If we do this, the boundaries of our set can become imprecise – and this is exactly what we need. In our “tall person” example, we could for instance define that Andrew with his height of 1.80 m gets a membership value of 1.0 in the set of “tall person”, whereas Bob with his 1.79 m gets a slightly smaller membership value of let’s say 0.95. This way, we avoid the problem of having to define a sharp border.

Figure 1 illustrates this difference between crisp and fuzzy sets. The x-axis shows different values (e.g., different heights) and the y-axis represents the membership in a fuzzy set. When we use crisp sets (gray line), we are only allowed to use memberships of 0 and 1. We therefore necessarily have some sharp borders. If we use fuzzy sets instead (black line), we can get a softer border. Whereas for crisp sets there is a sudden “jump” in the membership value, we get a smooth transition for the fuzzy set. It is exactly this sudden jump that caused our original problem and by using fuzzy sets, we can get rid of it.

This idea can also be applied to our simple star-shaped sets, which represent concepts in a conceptual space: We take a simple star-shaped set and call it the “core” of a concept. Note that this core is a crisp set. All points that lie inside this core get a membership value of 1.0 to the concept. All other points get a membership value based on their distance to the core – the smaller the distance, the higher the membership.

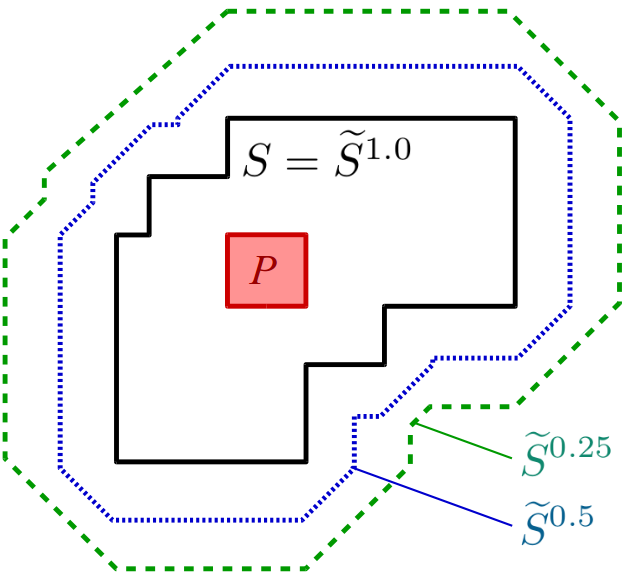
Figure 2 illustrates this idea. It shows the simple star-shaped set S along with two of its so-called “α-cuts”. An α-cut is the crisp set of all points with a membership value of at least α. The blue line indicates the α-cut for 0.5 (also called the 0.5-cut) and encloses the region of all points that have a membership value of 0.5 or higher. The green line illustrates the 0.25-cut, i.e. the set of all points with a membership value of 0.25 or higher. By using fuzzy simple star-shaped sets, we can therefore take care of imprecise concept boundaries: There is no sudden jump with respect to the membership to a concept, but a soft transition.

So let me summarize the key ideas of my formalization:

• Correlations between different domains are an important part of concepts. However, we cannot geometrically represent these correlations if we use convex sets (see here).
• If we only require our sets to be star-shaped, we are able to geometrically represent correlations between domains (see here).
• We define the core of a concept as a set of axis-parallel cuboids that have a non-empty region of overlap (see here).
• We use fuzzy sets to represent imprecise concept boundaries. Each point in the conceptual space is assigned a membership value to the given concept based on its distance to this concept’s core (where larger distances imply smaller membership values).

That’s already it from a high-level perspective. If you’re interested in the exact details of these definitions, please feel free to look at my paper [2].

References

[1] Zadeh, Lotfi A. “Fuzzy Sets” Information and Control, 1965.

[2] Bechberger, Lucas and Kühnberger, Kai-Uwe. “A Thorough Formalization of Conceptual Spaces” 40th German Conference on Artificial Intelligence, 2017.