Recently, another one of my papers [1] (look at the preprint here) has been accepted at the German Conference on Artificial Intelligence. It is a quite technical paper with a lot of formulas, but I’ll try to illustrate the overall high-level idea in this and one or two future blog posts.
Today I would like to talk about the starting point of the research presented in this paper: The observation that convex regions in a conceptual space are highly problematic if we want to represent correlations between domains.
In one of my first posts, I have introduced the framework of conceptual spaces. Just a quick recap: A conceptual space is spanned by a set of quality dimensions (e.g., hue, pitch, temperature, weight) that are grouped into domains (e.g., the color domain, which consists of the dimensions hue, saturation, and brightness). Each point in this space corresponds to a single observation and regions in this space correspond to properties (like red) and concepts (like apple).
The distance between two points within a domain is computed by the Euclidean distance (i.e., the length of the straight line segment connecting them). The distance between two points in different domains is computed by the Manhattan distance (i.e., the sum of the individual distances). Figure 1 illustrates the difference between these two distance functions.
The intuition behind the Manhattan metric is as follows: If you live in Manhattan, where all the streets from a grid like the one in Figure 1, and you want to get from one point to the other, then you have to follow the streets. There’s no way of walking along the green line, because you can’t walk through the buildings. So the shortest way between the two points in Figure 1 is something like “6 blocks north and 6 block east”, which means 12 blocks in total.
One can define a betweenness relation of three points based on such a distance function: A point B is between a point A and a point C if and only if the distance between A and C is equal to the sum of the distances between A and B, and B and C, respectively. In a mathematical formula, this looks as follows:
Between(A,B,C) ⇔ (d(A,C) = d(A,B) + d(B,C))
Intuitively speaking, one could say that B is between A and C if and only if the overall way from A to B and then from B to C is not longer than going straight from A to C. Or in other words: Visiting B on the way from A to C is not a detour.
Let’s look again at Figure 1 to illustrate what this means: Let’s call the two end points A (the bottom left one) and C (the top right one). If we use the Euclidean distance, then only the points on the green line are between A and C. If we pick any other point (e.g., the one in the top left corner, let’s call it B), the equation from above will not hold: The distance from A to B is 6, and the distance from B to C is also 6, so the sum of them is 12 – which is more than the length of the green line (around 8.5).
However, if we decide to use the Manhattan distance, something strange happens: The top left corner is now also considered to be between A and C! As we just argued, the way from A to C via B has a length of 12. And as we said earlier, the distance of A and C under the Manhattan distance is also 12. Thus, our definition of betweenness is fulfilled. If you think about it for a bit, you will realize that this also holds for any other point in the rectangle spanned by the two points.
If we go back to the Manhattan example, we can think of this as follows: If you want to go from A (e.g., your workplace) to C (e.g., your home), it is not a detour to stop by at B (e.g., a supermarket) – you will have to walk 12 blocks anyways.
So as a short summary: Betweenness under the Euclidean distance is the line segment connecting two points. Betweenness under the Manhattan distance is the rectangle between two points.
Why is this relevant? Remember from the previous post on conceptual spaces, that Gärdenfors [2] has defined concepts as convex regions in a conceptual space. Remember also that we call a region convex if it fulfills the following requirement:
If we have two points A and C that both belong to this region R, then any point B that lies somewhere between A and C must also belong to R.
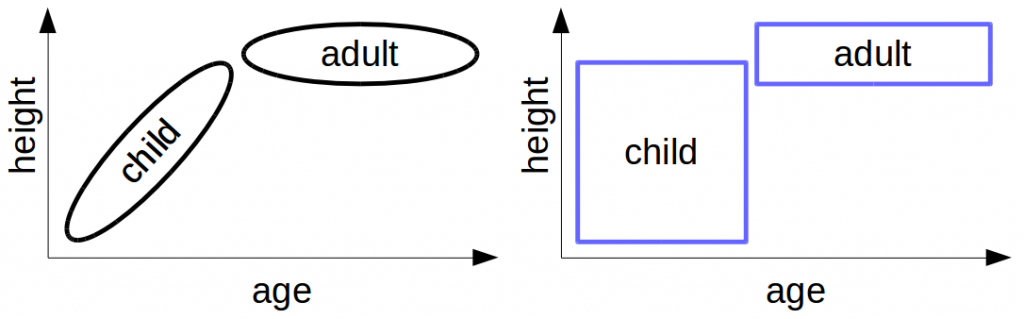
Let’s look at a simple example (Figure 2): If we would like to define the concepts of “adult” and “child” in a space consisting of the two domains “age” and “height”, we would probably draw something like in the left part of the figure. For children, there is a strong correlation between age and height (12 year old children tend to be taller than 3 year old children), whereas for adults there is no such correlation. To me it seems that this correlation of age and height in children is an relatively important piece of information.
As age and height belong to different domains, we should use the Manhattan distance to combine them. We also would like our concepts to be convex.The combination of these two requirements this causes some trouble:
If a point at the bottom left of the “child” concept and a point at the top right point of the “child” concept are both in this set, then the convexity requirement tells us that all points between these two should also be in the set. But as we discovered earlier, betweenness under the Manhattan distance is represented by a rectangle between two points. We are therefore forced to change our representation from the one in left part of Figure 2 to the one in the right part of Figure 2. Now we have convex sets, but we paid a high price for this – we lost all information about the correlation of age and height in the “child” concept. And I would argue that this is actually some quite important piece of information that we lost there. This convex representation says that a three year old child with a height of 1.60 m is perfectly reasonable – completely contrary to our intuition.
This sets the stage for my scientific contribution in the aforementioned paper. In my opinion, this is a serious problem that cannot be ignored and that needs to be resolved somehow. In my next post, I will sketch a solution to this problem, that I have developed over the past months. Stay tuned!
References
[1] Bechberger, Lucas and Kühnberger, Kai-Uwe. “A Thorough Formalization of Conceptual Spaces” 40th German Conference on Artificial Intelligence, 2017.
[2] Gärdenfors, Peter. Conceptual Spaces: The Geometry of Thought. MIT Press, 2000.
3 thoughts on “Convex regions in a conceptual space are problematic”