In the past two blog posts, we have discussed both transfer learning and multi-task learning for a four-dimensional target space of shapes. We observed that sketch-based networks seem to work better than photograph-based networks and that multi-task learning gave better results than transfer learning. Today, we’ll try to see whether these results also generalize to target spaces of different dimensionality.
Methods
I’ve conducted a relatively straightforward generalization experiment in order to test the behavior of different approaches, dependent on the number of dimensions in the target similarity space. The following contestants will enter the race:
- The Zero Baseline always predicts the origin and serves as a lower performance bound.
- The Transfer (Photos) setup is a lasso regression (with β = 0.005) trained on top of the pre-trained inception-v3 network [1].
- The Transfer (Sketches) approach corresponds to the pre-trained Small configuration of our sketch recognition network with a subsequent lasso regression (using β = 0.02).
- The Multi-Task (Sketches) setup is the Default configuration of our sketch recognition network, which is trained jointly on sketch recognition and the mapping task (using a mapping weight of 0.0625).
Essentially, these are the overall configurations which gave the best results in our experiments on the four-dimensional similarity space. We simply take the hyperparameter configurations as identified earlier and re-train those systems (only the lasso regression in the transfer learning case, but the whole network in the multi-task learning setting) on other target similarity spaces, without doing any further hyperparameter optimization. This is mainly done to save us some time, but can also be seen as a “stonger” test of generalization, since we don’t further optimize our results.
For evaluation purposes, we use the mean squared error (MSE), the mean Euclidean distance (MED) between prediction and ground truth, and the coefficient of determination R². As usual, results are aggregated across all folds in a five-fold cross validation.
Results
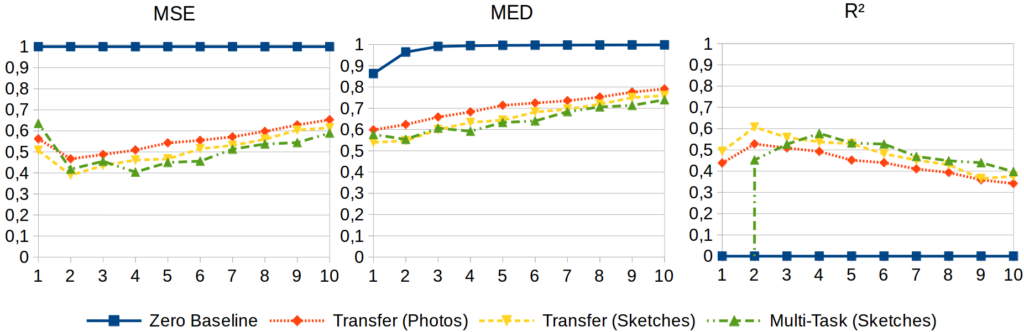
Figure 1 displays the results of this generalization experiment with respect to the three evaluation metrics. The same general tendencies can be observed across these three plots:
Firstly, all approaches considerably outperform the Zero Baseline, independent of the number of dimensions. Secondly, the Transfer (Sketches) approach slightly, but consistently outperforms the Transfer (Photos) setup on all target spaces. Thirdly, both transfer learning approaches reach their optimal performance level for a two-dimensional similarity space. Fourthly, performance tends to decrease with an increasing number of dimensions. Finally, the Multi-Task (Sketches) setup performs better than the transfer learning approaches on target spaces with at least four dimensions, but loses its advantage for lower-dimensional spaces. For a one-dimensional space, it performs poorer than the Transfer (Photos) approach with respect to the MSE, and even worse than the Zero Baseline with respect to R².
Discussion
So what do these results tell us?
Apparently, there is a certain trade-off with respect to the number of dimensions: If the target space is too high-dimensional, the mapping task becomes too difficult, hence we observe poor performance. On the other hand, a one-dimensional similarity space also yields clearly sub-optimal performance, probably because it is relatively unstructured. The results reported above thus confirm our earlier observations on the NOUN data set, where also a two-dimensional target space was optimal in a transfer learning setting.
While the transfer learning approaches show relatively “regular” generalization patterns, the multi-task learner seems to be more sensitive to the number of dimensions. One may speculate that this is based on the fixed value for the mapping weight, which may make overfitting more likely in low-dimensional target spaces. Nevertheless, the overall pattern of multi-task learning being better than transfer learning and the photograph-based network performing worst remains intact for most target spaces, thus giving further support to our prior observations.
Outlook
So while the results of this generalization experiment are certainly interesting by themselves, what are the logical next steps?
Clearly, even when considering lower-dimensional spaces (where the regression problem becomes somewhat easier), our results are still considerably worse than the ones obtained by Sanders and Nosofsky [2]. However, they used a considerably larger data set (360 instead of 60 stimuli) and a more complex network architecture. It may thus be worthwhile to collect additional similarity ratings for a larger set of stimuli and then to re-conduct our machine learning experiments. Also looking into more complex network architectures and smarter data augmentation, pre-training, and regularization schemes may pay off in terms of improved performance.
Since my PhD is slowly coming to an end, I will however not go further in this direction. Instead, I will use my remaining time to explore the use of autoencoders instead of classifiers. I have already sketched in one of my first posts in this series that one can also use a decoder network instead of a classification layer in order to learn a useful hidden representation. The experiments with respect to this approach are currently still ongoing, but I’m likely to have some first results in the next 2-3 weeks. So stay tuned!
References
[1] Christian Szegedy, Vincent Vanhoucke, Sergey Ioffe, Jon Shlens, and Zbigniew Wojna. Rethinking the Inception Architecture for Computer Vision Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition, 2016, 2818-2826.
[2] Sanders, C. A. & Nosofsky, R. M. Using Deep-Learning Representations of Complex Natural Stimuli as Input to Psychological Models of Classification Proceedings of the 2018 Conference of the Cognitive Science Society, Madison., 2018

One thought on “Learning To Map Images Into Shape Space (Part 7)”