This week, the first paper of my PhD research [1] has been accepted for publication (you can take a look at the preprint here). I would like to seize the opportunity and explain here on a high level what this paper is about.
I’ve explained in a previous post what a conceptual space looks like. The aforementioned paper discusses the question posed in the title of this post: “Where do the dimensions of a conceptual space come from?”
For some simple domains it is quite clear which dimensions one should use to describe them: For instance, we already have a relatively good understanding how to describe colors with three-dimensional models. There’s the RGB system used for computer monitors (with three dimensions corresponding to the degree of presence of the basic colors Red, Green, and Blue), the more cognitively inspired HSB model (with the three dimensions Hue, Saturation, and Brightness), and many more. So when we want to define a conceptual space that should be able to represent colors, we already have a relatively good idea which kind of dimensions we could use.
For other domains, however, things are a bit more complicated: For instance, it is relatively unclear how the shape domain is structured – which dimensions should we use to describe different shapes? As it turns out, it is surprisingly hard to answer this question. And the question about the underlying dimensions gets even harder when we think about more abstract concepts like “friendship” – what kind of dimensions would we need to describe friendship?
In the aforementioned paper, I focus on the shape example (because it’s much simpler than the friendship example). My basic proposal is the following: Let’s use unsupervised machine learning (more specifically, neural networks) to learn dimensions that are useful for describing shapes.
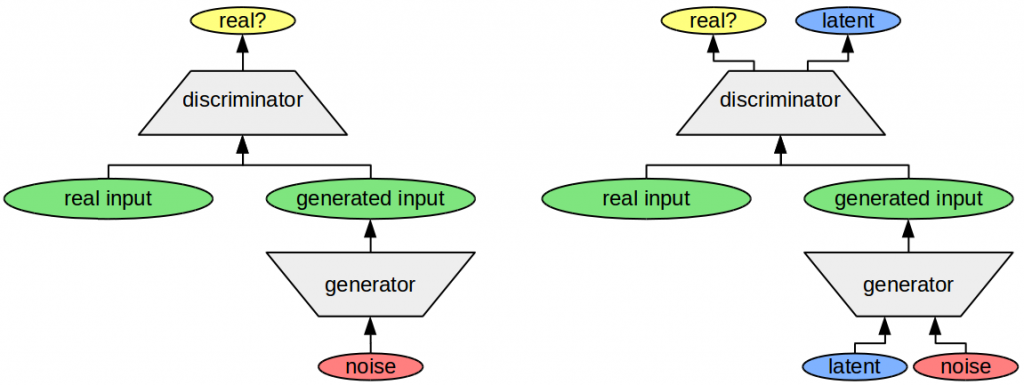
This should roughly work as follows (more details are in the paper itself): We take a data set consisting of shape images (i.e., images of circles, triangles, rectangles, etc.) and we train a neural network to generate images that are similar to the ones in this data set. Another neural network tries to discriminate between generated and real images. If the generator network is able to fool the discriminator network, then we assume that the former is capable of generating realistic images. This is the principle of the GAN framework [2] which is depicted in the left part of Figure 1. The noise vector that is used as input to the generator network can be thought of as a list of randomly chosen numbers which the generator network has to convert into an image.
The right part of Figure 1 shows an extension of this framework which is called InfoGAN [3]. Here, some of the numbers that the generator receives as input have to be reconstructed by the discriminator (these numbers are called “latent variables”). That is, the discriminator has to figure out which numbers the generator used to create the image in the first place. As it turns out, these numbers end up describing meaningful properties of the images. For instance, when this system was trained with images of hand-written digits, the latent variables could be interpreted as the width and orientation of the digit.
My proposal is to use exactly this InfoGAN system on a data set of shapes, hoping that the latent variables also will get some interpretable meaning. Each of these variables could then be used as a dimension of the shape domain and the InfoGAN network could be used to compute the coordinates of a given shape in this shape domain.
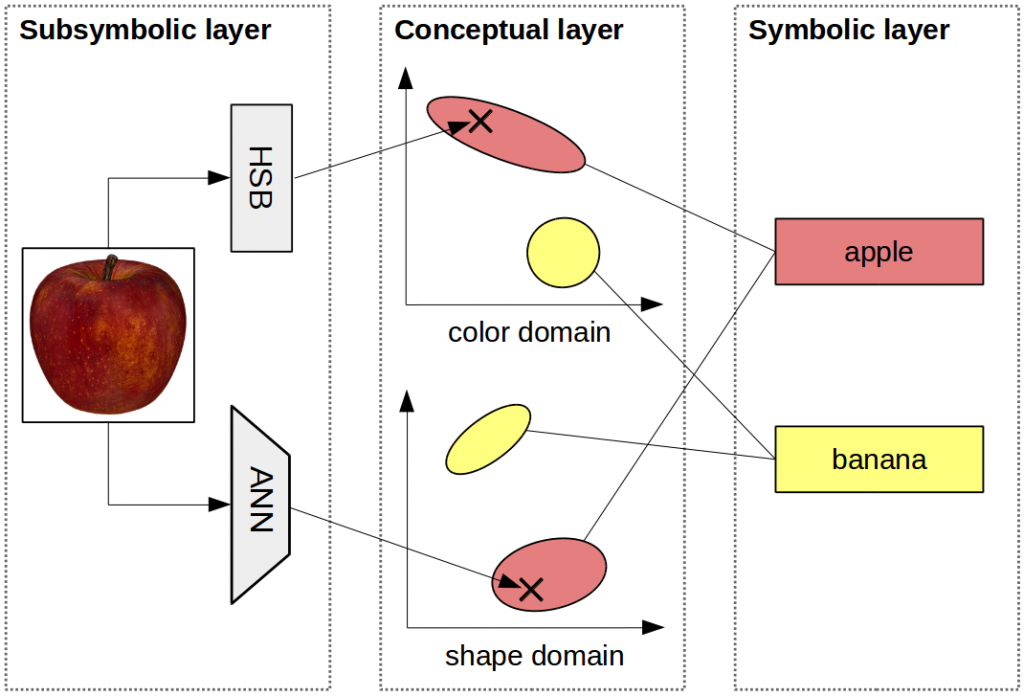
In the end, we would then have two kinds of domains: Manually built ones (like color) and learned ones (like shape). Figure 2 shows how this could look like. For each input object (e.g., an image of an apple), we derive its coordinates in the color space by extracting the HSB coordinates with some hard-coded program. The object’s coordinates in the shape domain, however, are extracted by the InfoGAN (labeled in Figure 2 as ANN for Artificial Neural Network). The definition of concepts (like apple and banana) can then take place as usual within this conceptual space.
Final Disclaimer: This is of course only a research proposal – I haven’t had the time yet to implement and test this. So right now I don’t know whether this will actually work – I’m planning to investigate this in practice over the next few months.
References
[1] Bechberger, Lucas and Kühnberger, Kai-Uwe. “Towards Grounding Conceptual Spaces in Neural Representations.” Twelveth International Workshop on Neural-Symbolic Learning and Reasoning, 2017.
[2] Goodfellow, Ian, et al. “Generative Adversarial Nets.” Advances in Neural Information Processing Systems, 2014.
[3] Chen, Xi, et al. “InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets.” Advances in Neural Information Processing Systems, 2016

4 thoughts on “Where do the dimensions of a conceptual space come from?”