I’ve already talked about InfoGAN [1] a couple of times (here, here, and here). InfoGAN is a specific neural network architecture that claims to extract interpretable and semantically meaningful dimensions from unlabeled data sets – exactly what we need in order to automatically extract a conceptual space from data.
InfoGAN is however not the only architecture that makes this claim. Today, I will talk about the β-variational autoencoder (β-VAE) [2] which uses a different approach for reaching the same goal.
For the sake of simplicity, I will only talk about images in this text as both InfoGAN and β-VAE are usually applied to image data.
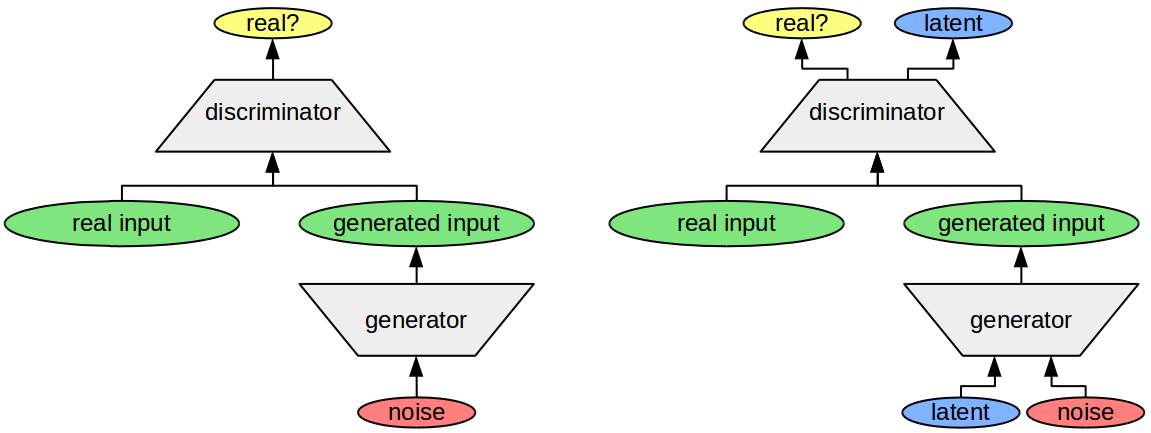
The right part of Figure 1 shows again the structure of the InfoGAN architecture. There are two networks involved: The generator uses a latent code plus some random noise in order to generate realistic images. The discriminator network tries to distinguish between real and generated images and has the additional task to reconstruct the latent code. If training is successful, then the individual dimensions within the latent code correspond to interpretable features of the data set.
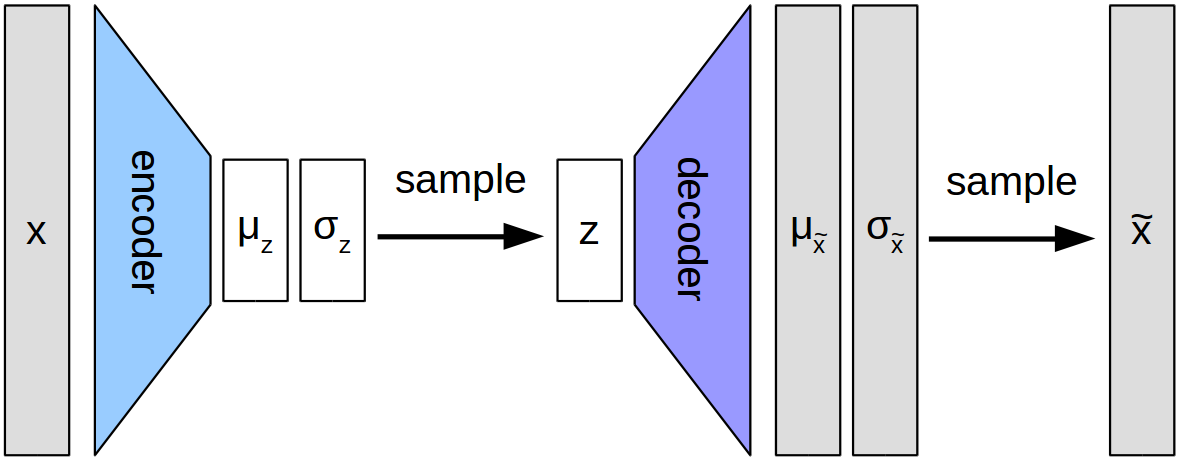
The architecture of the β-VAE is shown in Figure 2. As one can see, the overall setup consists also here of two networks (highlighted with colors): The encoder takes an image (here denoted by x) and transforms it into a latent representation, whereas the decoder takes this latent representation and tries to reconstruct the original image. One can thus say that the encoder in β-VAE corresponds to the discriminator in InfoGAN and that the decoder in β-VAE corresponds to the generator in InfoGAN.
As you may have noticed, there is not a single latent code between the encoder and the decoder, but something more complicated. One of the properties that distinguishes β-VAE from regular autoencoders is the fact that both networks do not output a single number, but a probability distribution over numbers. More specifically, they use a normal distribution which can be described by its mean μ and its standard deviation σ. Figure 3 illustrates how such a normal distribution looks like.
So the networks output the mean μ and the standard deviation σ of a normal distribution over possible values. As we however need to use a single number as an input to the decoder network, we have to sample a single value z from this distribution. This is illustrated by the “sample” arrows in Figure 2.
How is the β-VAE architecture trained? There are two objectives:
On the one hand, one wants to minimize the reconstruction error: For any given image x that we first put through the encoder and afterwards through the decoder, we want the resulting reconstruction to be as similar as possible to the original x. In the β-VAE architecture, this is formulated as maximizing the probability of x under the probability distribution returned by the decoder.
On the other hand, we want to make sure that the individual entries of our latent representation z are interpretable. This is however hard to measure directly. If we assume that interpretable dimensions are independent from each other (one can e.g., manipulate the width of an object without changing anything about its height or its color), then we can however measure this independence and use it as a substitute for interpretability. This is exactly what is done in β-VAE: We try to minimize the difference between the distribution generated for z and an isotropic multivariate normal distribution (i.e., a normal distribution without any interactions between the individual dimensions). By doing so, we cause the individual entires of z to have a low correlation among each other, and hopefully this makes them more interpretable.
What I’ve explained to you so far is just the standard variational autoencoder (VAE) as described in [3]. Now where does the β come in?
In standard VAE, the two learning objectives are combined by simply adding them up. This means that both objectives are equally important. In β-VAE, however, a factor β is introduced that influences the relative weight of the second objective: A higher value of β puts more emphasis on the statistical independence than on the reconstruction. As it has been observed in experiments, this stronger focus on statistical independence helps a lot in making the latent code more interpretable. However, as focusing on statistical independence automatically means to care less about good reconstructions, we have to pay for the increased interpretablity with reduced reconstruction quality.
I’ll leave my discussion about β-VAE at this level of abstraction. If you want to dive in deeper and look at the underlying math, I can recommend [4] which lays out the mathematical derivation of the VAE training objective in a nice step-by-step manner.
Why am I writing about β-VAE? Well, since it has also shown to be quite useful for extracting interpretable dimensions, I will use it as a competitor to InfoGAN with respect to my rectangle domain. Stay tuned for updates!
References
[1] Chen, Xi, et al. “InfoGAN: Interpretable Representation Learning by Information Maximizing Generative Adversarial Nets.” Advances in Neural Information Processing Systems, 2016
[2] Higgins, Irina et al. “β-VAE: Learning Basic Visual Concepts with a Constrained Variational Framework.” 5th International Conference on Learning Representations, 2017
[3] Kingma, D. P. & Welling, M. “Auto-Encoding Variational Bayes.” arXiv preprint arXiv:1312.6114, 2013
[4] Doersch, C. “Tutorial on Variational Autoencoders.” arXiv preprint arXiv:1606.05908, 2016
