It’s nice to have a mathematical definition of concepts in a conceptual space. It’s also nice that we can create new concepts based on old ones, for instance by intersecting them. But being able to talk about the relation of two concepts is certainly also useful. Last time, we talked about the size of a concept. We can use the size of concept to figure out that the concept of “animal” is more general than the concept of “Granny Smith” – simply because it is larger.
But there are also other ways of describing the relation of two concepts. Two of them, namely subsethood and implication, will be presented in today’s blog post.
Before I give you an idea about how subsethood and implication are defined in my formalization [1], let’s start with the following questions: “What does it mean if a concept is a subset of another concept? What does it mean if a concept implies another concept?”
Technically, if a set A is a subset of B, this means that all points which belong to A also must belong to B. If we transfer this to conceptual spaces, we find examples like the following: If apple is a subset of fruit, this means that all objects in the world that you would classify as being an apple also have to be classified as fruit. Or in other words: All apples are fruit – apple is a special kind of fruit. So basically, the subsethood relation gives us a way to talk about hierarchies of concepts: Granny Smith is an apple which is a fruit which is a type of food. Moreover, from this subsethood hierarchy we automatically get that Granny Smith is a fruit or that apple is a special kind of food.
What about implication? If the concept of apple implies the concept of red, this tells us that whenever you have an apple, you can directly deduce that it’s red. Or in other words: All apples are red. But wait a second, doesn’t that sound familiar? Haven’t we just said almost the same thing about subsethood?
I would say yes: In our conceptual spaces setting, implication and subsethood are practically the same thing: If Granny Smith is a subset of apple, then all Granny Smiths are apples. And if apple implies red, then all apples are red. The only difference in these two examples is that Granny Smith and apple are defined on many domains (color, shape, taste, size, etc.), whereas red is only defined on a single domain. But other than that, the mechanism is the same.
Therefore, I treat subsethood and implication interchangeably. In my approach, they’re the same thing: A implies B if and only if A is a subset of B. I think that this in itself is already an interesting insight.
Now there’s one additional twist to the idea which I’d like to share with you: “Well, that sounds kinda convincing… But what about tomatoes? Are they fruit or vegetables?”
Technically, from a biological point of view, tomatoes are fruit (see for instance Wikipedia), but they share many characteristics with vegetables and are often classified as such in everyday life. So how would we encode that in a conceptual space? Is the tomato concept a subset of the vegetable concept or a subset of the fruit concept?
As I use fuzzy sets to represent concepts, my solution to this problem is a fuzzy one: The tomato concept is a subset of both the vegetable and the fruit concept – to some degree. That means it is not a perfect subset of either of them, but has some considerable overlap with both.
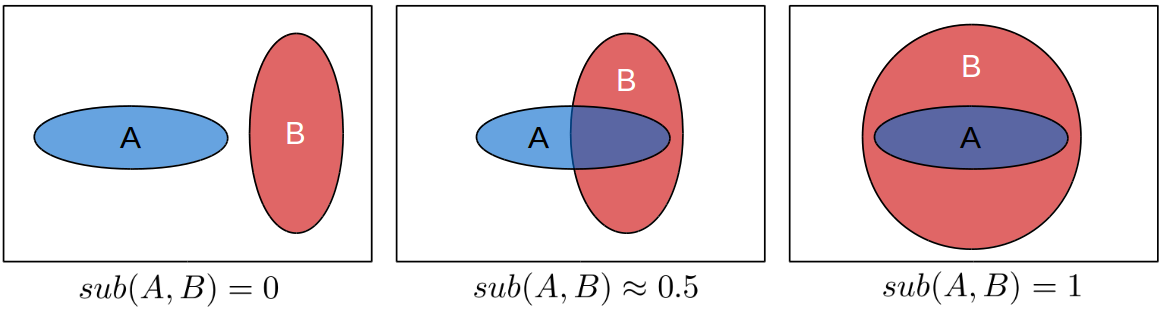
Figure 1 illustrates how such a degree of subsethood can look like in general. If you have two sets A and B and they do not have any intersection, you would probably say that A is not a subset of B at all. This corresponds to a degree of subsethood of zero.
On the other hand, if A is completely contained in B, you would probably say that A is definitely a subset of B. This corresponds to a degree of subsethood of one. So far, so normal.
Now if you observe a situation like in the middle of Figure 1, where A and B have some considerable overlap, you could argue that A is a subset of B to a degree of let’s say 0.5. The interpretation would be like “Well, it’s not really a subset in the strict sense, but a considerable part of it is contained in B, so it’s not like the two sets are not related at all.”
Mathematically, we can express this for example as follows [2]:
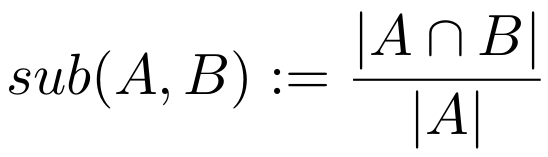The degree to which A is a subset of B is defined as the size of their intersection divided by the size of A. The degree of subsethood therefore measures the percentage of A that is also in B. If all of A is contained in B, then we get a value of one, if nothing that is in A is also in B, then we get a value of zero, and for all other cases, we get something between those two extremes. As we’ve previously already defined how to compute the intersection and the size of a concept, it’s also not too complicated to compute the degree of subsethood.
Coming back to the tomato example, this would mean that a layman might consider tomato to be a subset of vegetable to a degree of let’s say 0.8 (because it’s taste and appearance are similar to other vegetables) and a subset of fruit to a degree of maybe 0.2 (because of the biological information). So in principle, also the concepts that don’t fit neatly into any of the given categories can be taken care of.
References
[1] Lucas Bechberger and Kai-Uwe Kühnberger: “Measuring Relations between Concepts in Conceptual Spaces” Thirty-seventh SGAI International Conference on Artificial Intelligence, Cambridge/UK, December 2017.
[2] Kosko, B. (1992). Neural networks and fuzzy systems: a dynamical systems approach to machine intelligence/book and disk. Vol. 1Prentice hall.