A while ago, I introduced Logic Tensor Networks (LTNs) and argued that they are nicely applicable in a conceptual spaces scenario. In one of my recent posts, I described how to ensure that an LTN can only learn convex concepts. Today, I will take this one step further by introducing additional ways of defining the membership function of an LTN.
Radial Basis Function
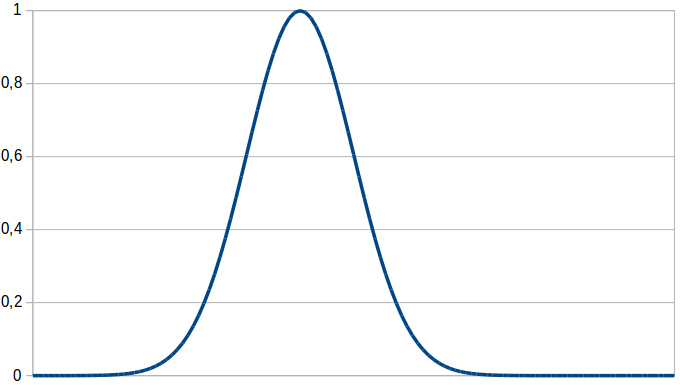
Figure 1 illustrates the shape of a radial basis function (RBF). It has the same shape as a normal distribution, but a maximum value of one. Remember that a normal distribution is a probability density function and that its integral therefore needs to be equal to one. In our case, we do not care about the size of the integral, but about the highest achievable value, which should be one. Therefore, the RBF basically is a scaled normal distribution.
The nice thing about using RBF is that we have the guarantee that the membership function is always convex – which is in line with Gärdenfors’ claim that concepts are represented by convex regions. Moreover, if the RBF is defined on multiple dimensions, its shape resembles that of a multivariate normal distribution. The entries of this distribution’s covariance matrix can be used to encode correlations between the different dimensions. This is quite nice from a representational point of view. Therefore, using an RBF as a membership function for concepts in the LTN framework seems to be worth a try.
Prototype
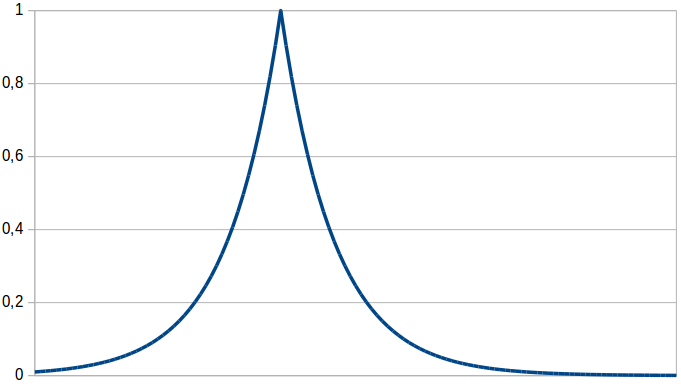
Another potential membership function is based on Gärdenfors’ work: On the one hand, he proposes to represent each concept by a prototypical point in the conceptual space, and of the other hand he argues that conceptual similarity should be computed as an exponentially decaying function of distance in the conceptual space. The membership function resulting from combining these two proposals is shown in Figure 2 and based on the following formula:
![]()
The membership of a point x to a concept is based on the distance d(x,p) to this concept’s prototype p. The exponential decay (whose strength is influenced by the sensitivity parameter c) makes sure that only points close to the prototype get a high degree of membership. When computing the distance between the given point and the prototype, one can adjust the influence of the different dimensions by putting weights on them. However, this approach is not capable of representing correlations. Nevertheless, as it is quite directly based on Gärdenfors’ basic assumptions, it might be an interesting competitor.
Cuboid
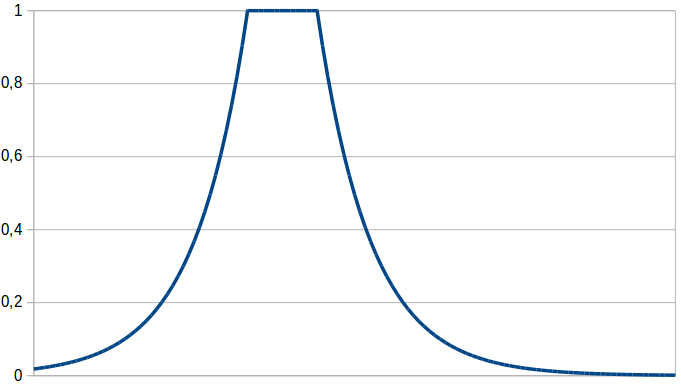
After having invested a considerable amount of time into my mathematical formalization of conceptual spaces, I am of course also eager to use it. Therefore, my last proposal is the membership function for concepts from my formalization. It uses an exponentially decaying function of the distance of the given point to the concept’s core, which is described by a cuboid. As it turns out, the “Prototype” membership function proposed above is just a special case of this (with the prototypical point being the limiting case of a cuboid).
As I have argued before, the membership function based on a single cuboid is convex. If we use multiple cuboids and make sure that they all overlap, we get a star-shaped set which is able to encode correlations. Moreover, this proposed membership function has an additional advantage: Once we have learned the concepts by using LTNs, we can use the full mathematical machinery of my formalization in order to apply operations on these concepts and to reason with them. This could be therefore a nice connection between my theoretical formalization and practical machine learning experiments.
Next Steps
Of course, these definitions are so far only definitions. It is not yet clear how well the LTN framework works with these membership functions. Therefore, my next step is to run some experiments and to analyze whether there are any differences between the original membership function, its convex variant, and the definitions proposed above. If I find any differences, it will be interesting to see which definition works best under which circumstances and to think about possible reasons for this.
